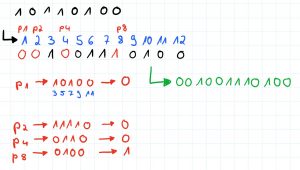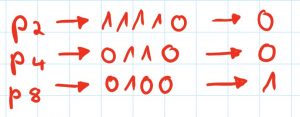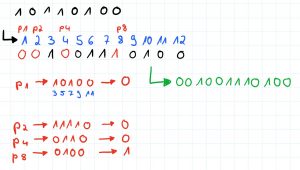Pflanzen pflanzen Pflanzen!
Heute habe ich den Lithops zum ersten Mal gegossen. Bei Sukkulenten merkt man dass sie Wasser benötigen, wenn die „Blätter“ weicher und manchmal etwas schrumpelig werden.
Außerdem hab ich die Steindekoration auf der Kakteen-Erde mit Sand ergänzt. Jetzt kann der kleine Lithops sich richtig wohl fühlen! 🙂
Generelle Informationen zum Lithops hier.
Der Hammingcode ist ein fehlerkorrigierender Code, bei dem bestimmte Bits der Überprüfung der restlichen Bits dienen.
Ich werde die Codierung an dem Beispiel einer 8-Bit Zahl zeigen: 10110100
Die „Hamming Code“-Bits befinden sich immer an den Stellen 2n, bei einer 8-Bit Zahl also an den Stellen 1, 2, 4 und 8, somit muss die Länge auf 12 Bits erhöht werden.
Die „Hamming-Code“-Bits nenne ich p1, p2, p4 und p8.
An die restlichen Stellen schreibe ich meine 8-Bit Zahl:
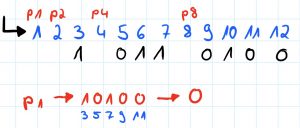
Nun möchte ich heraus finden, welches Bit ( 1 oder 0) an der Stelle p1 steht. Dafür schreibe ich jedes 2. Bit auf, angefangen bei p1. Also die Bits an den Stellen 3, 5, 7, 9 und 11.
Ist die Anzahl der 1en in dieser Bitfolge gerade, so ist p1 = 0.
Ist die Anzahl der 1en in dieser Bitfolge ungerade, so ist p1 = 1.
In diesem Fall also 0.
Um p2, p4 und p8 zu ermitteln wenden wir das gleiche Prinzip an, nur dass wir bei der Berechnung von p2 immer 2 Bits in die Bitfolge schreiben, zwei überspringen, zwei Bits in die Bitfolge…
Bei p4 und p8 dasselbe Muster aber mit 4 bzw. 8 Bits.
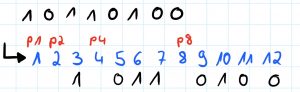
Die folgenden bunt markierten Bits sind ausschlaggebend für die Bitfolgen zur Ermittlung von p1, p2, p4 und p8.
Somit ergeben sich für p2, p4 und p8 folgende Bits:
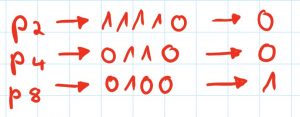
Nun können wir p1, p2, p4 und p8 in unsere 12-Bit Zahl eintragen und erhalten somit eine Hamming-Codierte Zahl.
